Model Cournota to klasyczna koncepcja w mikroekonomii opisująca konkurencję między dwoma producentami, którzy decydują o wielkości produkcji niezależnie i jednocześnie. Przedstawiony tutaj opis obejmuje genezę teorii, matematyczną analizę oraz praktyczne implikacje i rozszerzenia. Celem tekstu jest szczegółowe wyjaśnienie mechanizmu działania modelu, jego ograniczeń oraz porównanie z innymi modelami oligopolu, takimi jak Bertrand czy Stackelberg.
Geneza i podstawowe założenia modelu
Model powstał na początku XIX wieku dzięki pracom francuskiego matematyka i ekonomisty Cournota. Jego analiza dotyczyła rynków, na których występują tylko dwaj producenci — stąd nazwa duopol. Podstawowe założenia klasycznego modelu Cournota są następujące:
- Na rynku działają dokładnie dwie firmy.
- Obie firmy decydują o wielkości produkcji (ilości) jednocześnie i niezależnie.
- Cena rynkowa jest malejącą funkcją łącznej ilości dostarczonej na rynek przez obie firmy (funkcja popytu).
- Obie firmy maksymalizują zysk przy znanej funkcji kosztów, zwykle zakłada się koszty krańcowe stałe lub liniowe (koszty).
- Firmy przyjmują, że decyzja konkurenta nie reaguje na zmianę ich własnej decyzji (przyjmują produkcję konkurenta jako daną przy podejmowaniu decyzji).
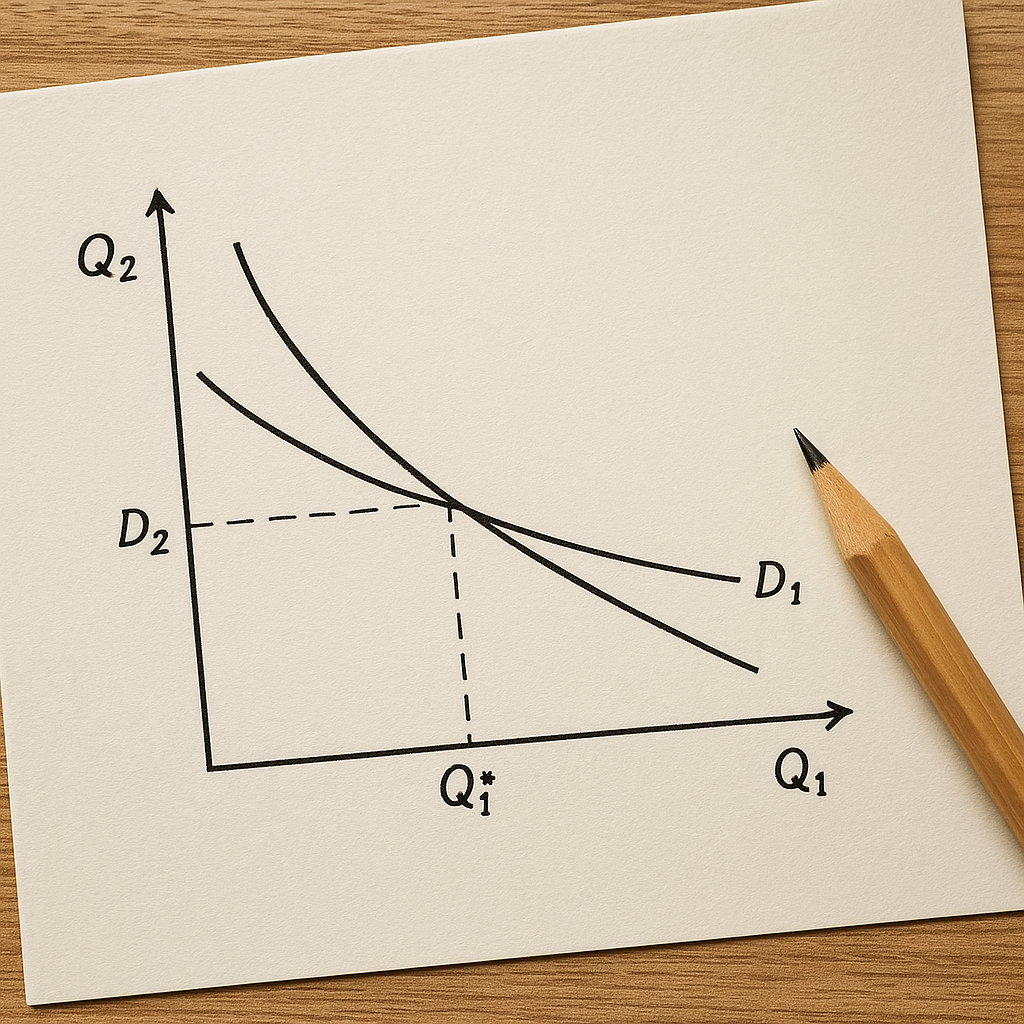
Konsekwencją tych założeń jest analiza reakcyjnych funkcji przedsiębiorstw i poszukiwanie punktu, w którym obie strategię są optymalne jednocześnie. Taki punkt to równowaga Cournota, która jest przykładem równowagi typu Nash w grach statycznych, gdzie strategie to poziomy produkcji.
Matematyczna analiza modelu: równowaga ilościowa
Aby zobrazować mechanizm działania modelu, rozważmy prosty, lecz standardowy przypadek: liniową funkcję popytu P(Q) = a − bQ, gdzie Q = q1 + q2, a > 0, b > 0, oraz koszty krańcowe obydwu firm równe c (może być równe zero). Zysk firmy 1 to π1 = [P(Q) − c] q1 = [a − b(q1 + q2) − c] q1. Analogicznie dla firmy 2.
Wyprowadzenie reakcyjnych funkcji
Aby znaleźć optymalną strategię firmy 1, maksymalizujemy π1 względem q1 traktując q2 jako stałe:
∂π1/∂q1 = a − b(q1 + q2) − c − b q1 = a − c − 2b q1 − b q2 = 0.
Stąd reakcyjna funkcja firmy 1 to q1 = (a − c − b q2) / (2b). Analogicznie reakcyjna funkcja firmy 2 to q2 = (a − c − b q1) / (2b). Obie funkcje wyrażają optymalną ilość produkcji jednej firmy jako funkcję produkcji drugiej firmy — jest to centralny element modelu Cournota: analiza wzajemnych reakcji (reakcja).
Równowaga Cournota
Rozwiązując układ dwóch równań reakcyjnych otrzymujemy równowagę:
q1* = q2* = (a − c) / (3b),
więc łączna wielkość produkcji Q* = 2(a − c) / (3b), a cena rynkowa P* = a − bQ* = a − 2(a − c)/3 = (a + 2c)/3. Zyski każdej firmy wynoszą π1* = π2* = [(P* − c) q1*] = [(a − c)^2 / (9b)].
Ta prosta analiza ukazuje kilka istotnych wniosków:
- W równowadze Cournota każda firma wytwarza więcej niż w monopolu (gdzie monopol produkuje (a − c) / (2b)), ale mniej niż w doskonałej konkurencji (gdzie cena = koszty krańcowe).
- Wynik rynkowy leży pomiędzy rozwiązaniem monopolu a doskonałej konkurencji: cena jest niższa niż monopolistyczna, lecz wyższa niż cena konkurencji doskonałej.
- Im większa liczba firm, tym bardziej wynik zbliża się do konkurencji doskonałej (rozszerzenie modelu Cournota na n firm).
Rozszerzenie na n firm
Dla n identycznych firm o stałych kosztach krańcowych c i tej samej funkcji popytu P(Q) = a − bQ, równowaga Cournota daje q_i = (a − c) / [(n + 1) b]. Stąd Q = n(a − c) / [(n + 1) b]. W granicy n → ∞ mamy Q → (a − c)/b, co odpowiada wynikowi konkurencji doskonałej.
Właściwości ekonomiczne i porównania z innymi modelami
Model Cournota pozwala na porównanie różnych struktur rynkowych. Kluczowe wnioski to:
- W porównaniu z modelem Bertrand (konkurencja w cenach), przy jednorodnych produktach i zerowych kosztach krańcowych konkurenci w Bertrand osiągają wynik równy konkurencji doskonałej (cena = koszt krańcowy), podczas gdy Cournot daje wyższą cenę. Różnica wynika z wyboru zmiennej strategicznej (ilość vs cena).
- Model Stackelberg wprowadza sekwencję decyzji: lider wybiera ilość pierwszy, a potem na jego decyzję reaguje naśladowca. Lider zwykle osiąga wyższy zysk niż w Cournot, a całkowita produkcja może się różnić w zależności od parametrów.
- Równowaga Cournota jest równowagą Nash — żadna z firm nie może jednostronnie poprawić swojego wyniku zmieniając produkcję przy założeniu produkcji konkurenta.
Warto zwrócić uwagę na efekty dobrobytu społecznego: konsument zyskuje względem monopolu, ale traci względem konkurencji doskonałej. Z punktu widzenia efektywności produkcja jest niższa niż społecznie optymalna, co generuje stratę dobrobytu (deadweight loss).
Asymetrie i koszty różne dla firm
Jeżeli firmy mają różne koszty (c1 ≠ c2), równowaga Cournota generalnie daje produkcję większą dla firmy z niższymi kosztami. Reakcyjne funkcje przestają być symetryczne, a obliczenia algebraiczne prowadzą do q1* = (a − 2b c1 + b c2) / (3b) w pewnych układach (dla liniowego popytu). Asymetria kosztów może prowadzić do znacznych różnic w zyskach i udziale rynkowym.
Rozszerzenia, ograniczenia i zastosowania empiryczne
Model Cournota jest fundamentem teorii oligopolu, ale jego zastosowanie wymaga zrozumienia ograniczeń i możliwych rozszerzeń. Poniżej omówiono wybrane modyfikacje i aspekty empiryczne.
Dynamiczne aspekty i powtarzane gry
Model statyczny zakłada jednorazowe decyzje. W praktyce firmy konkurują przez dłuższy czas. Gry powtarzane wprowadzają możliwość karania odchylenia od współpracy i umożliwiają osiąganie wyników bliższych monopolu poprzez strategie wypracowane na przestrzeni czasu. Modele te wykorzystują pojęcia takie jak równowaga subgier i strategie trigger.
Niepewność, informacja i kontrakty
Realistyczne rynki charakteryzują się niepewnością co do kosztów, popytu czy reakcji konkurentów. Modele z niepełną informacją analizują, jak asymetria informacji wpływa na wybór strategii i strukturę rynku. Mechanizmy sygnalizowania i screening są istotne przy badaniu wejścia nowych firm czy decyzji inwestycyjnych.
Produkty różnicowane
Klasyczny model zakłada dobra homogeniczne. Jeśli produkty są zróżnicowane, reakcje firm i równowaga są zmienione — konkurencja jest mniej intensywna, a ceny mogą być wyższe. Model Cournota daje wtedy mniej agresywne wyniki, ale analiza wymaga zastosowania funkcji popytu zależnych od obu poziomów produkcji i stopnia substytucyjności produktów.
Empiryczne zastosowania
W literaturze empirycznej model Cournota bywa używany do estymacji zachowań firm w branżach z dominacją kilku dużych producentów, jak przemysł samochodowy, energetyczny czy chemiczny. Badania porównują parametry reakcyjnych funkcji z danymi rynkowymi, oceniają siłę konkurencji i efekty wejścia kolejnych firm na rynek. W praktyce często trzeba uwzględnić czynniki takie jak ograniczenia pojemnościowe, wieloetapowa produkcja czy regulacje.
Praktyczne implikacje polityki gospodarczej i decyzji firm
Model Cournota dostarcza narzędzi analitycznych pomocnych przy formułowaniu polityki konkurencji i strategii korporacyjnych. Niektóre zastosowania praktyczne obejmują:
- Ocena skutków koncentracji rynku: symulacje Cournota pozwalają przewidzieć, jak fuzje wpływają na ceny i produkcję.
- Analiza wpływu subsydiów lub podatków na produkcję i dobrobyt społeczeństwa.
- Strategie ilościowe firm: decyzja o zwiększeniu mocy produkcyjnej lub ograniczeniu produkcji w krótkim i długim okresie.
Regulatorzy używają uproszczonych modeli Cournota do szacowania, czy zmiana struktury rynku doprowadzi do znaczącego pogorszenia warunków konkurencji. Firmy natomiast wykorzystują intuicję płynącą z modelu dla planowania produkcji i przewidywania reakcji konkurentów.
Ograniczenia modelu i krytyka
Mimo swojej elegancji i przejrzystości model Cournota bywa krytykowany za nadmierne uproszczenia. Najważniejsze zarzuty to:
- Założenie jednorazowych, jednoczesnych decyzji — często nierealistyczne w sektorach, gdzie firmy podejmują decyzje sekwencyjnie.
- Homogeniczność produktów i brak kosztów wejścia/wyjścia z rynku.
- Ignorowanie asymetrii informacji i niepewności, które wpływają na rzeczywiste strategie przedsiębiorstw.
- Stałe koszty krańcowe w wielu prostych modelach — rzeczywiste funkcje kosztów bywają bardziej złożone.
Mimo to model pozostaje cennym narzędziem dydaktycznym i analitycznym, służąc jako punkt wyjścia do bardziej zaawansowanych modeli oligopolu. Zrozumienie mechanizmu reakcji i równowagi ilościowej pomaga interpretować zachowania firm i przewidywać kierunek zmian rynkowych.
Dalsze kierunki badań i zastosowań
Współczesne badania rozwijają klasyczny model Cournota w wielu kierunkach: integrują asymetrię informacji, dynamikę inwestycji i innowacji, wprowadzają ograniczenia pojemności, analizują rynki sieciowe i platformy cyfrowe. Modele empiryczne wykorzystują techniki estymacji strukturalnej, aby lepiej dopasować teorię do danych rynkowych.
- Analiza wpływu technologii i innowacji na konkurencję ilościową oraz zmianę kosztów krańcowych.
- Modele wieloetapowe łączące decyzje inwestycyjne z późniejszą konkurencją ilościową.
- Zastosowania do rynków usług, gdzie wydajność i skala mają istotne znaczenie dla strategii produkcyjnej.
Model Cournota, choć prosty, pozostaje fundamentem zrozumienia konkurencji między dużymi graczami i dostarcza intuicji przydatnej zarówno w teoretycznych, jak i praktycznych analizach rynku. Jego rozszerzenia pozwalają na dostosowanie do złożonych sytuacji gospodarczych i pomagają w formułowaniu decyzji biznesowych i regulacyjnych.