Model CAPM (Capital Asset Pricing Model) jest jednym z najbardziej znanych i szeroko wykorzystywanych narzędzi w teorii finansów. Jego podstawowym celem jest wyjaśnienie relacji między oczekiwaną stopą zwrotu a ryzykiem inwestycyjnym, a także ustalenie wymaganej stopy zwrotu dla pojedynczego aktywa w kontekście portfela rynkowego. W artykule omówione zostaną geneza i główne założenia modelu, jego formalna postać i interpretacja, wyniki badań empirycznych oraz praktyczne zastosowania i ograniczenia tego podejścia.
Geneza i kluczowe założenia
Model CAPM został sformułowany niezależnie przez kilku autorów na początku lat 60. XX wieku, ze szczególnym wkładem Williama Sharpe’a, Johna Lintnera i Jacka Treynora. Jego powstanie było naturalnym rozwinięciem koncepcji optymalnego portfela zaproponowanej przez Harry’ego Markowitza, która opierała się na teorii mean-variance. CAPM upraszcza i rozszerza tę koncepcję, formułując prostą relację między oczekiwaną stopą zwrotu aktywa a jego relatywnym ryzykiem w kontekście rynkowym.
Do poprawnego działania modelu niezbędne są pewne założenia, które warto jasno wyliczyć. Najważniejsze z nich to:
- inwestorzy są racjonalni i maksymalizują użyteczność skoncentrowaną na średniej i wariancji stóp zwrotu;
- istnieje możliwość bezryzykownego lokowania kapitału po stałej stopie wolnej od ryzyka dla wszystkich uczestników rynku;
- inwestorzy mają jednorodne oczekiwania co do przyszłych stóp zwrotu, wariancji i korelacji aktywów;
- transakcje nie są obciążone kosztami ani podatkami; rynki są doskonale płynne;
- istnieje jednoperiodyczny horyzont inwestycyjny i możliwość swobodnego pożyczania/polegowania po stopie wolnej od ryzyka.
W praktyce te założenia są silne i rzadko w pełni spełnione, co wpływa na interpretację i zastosowalność wyników CAPM w rzeczywistych warunkach rynkowych. Niemniej model stanowi ważny punkt odniesienia i bench-mark dla licznych badań oraz decyzji inwestycyjnych.
Formuła modelu i matematyczna interpretacja
Podstawowa postać CAPM wyraża oczekiwaną stopę zwrotu z aktywa i jako sumę stopy wolnej od ryzyka oraz składnika premii zależnej od ryzyka systemowego. Matematycznie zapisuje się to jako:
E(Ri) = Rf + βi * [E(Rm) − Rf]
gdzie:
- E(Ri) — oczekiwana stopa zwrotu z aktywa i,
- Rf — stopa wolna od ryzyka,
- E(Rm) — oczekiwana stopa zwrotu z portfela rynkowego,
- βi — współczynnik beta aktywa i, definiowany jako cov(Ri, Rm) / var(Rm).
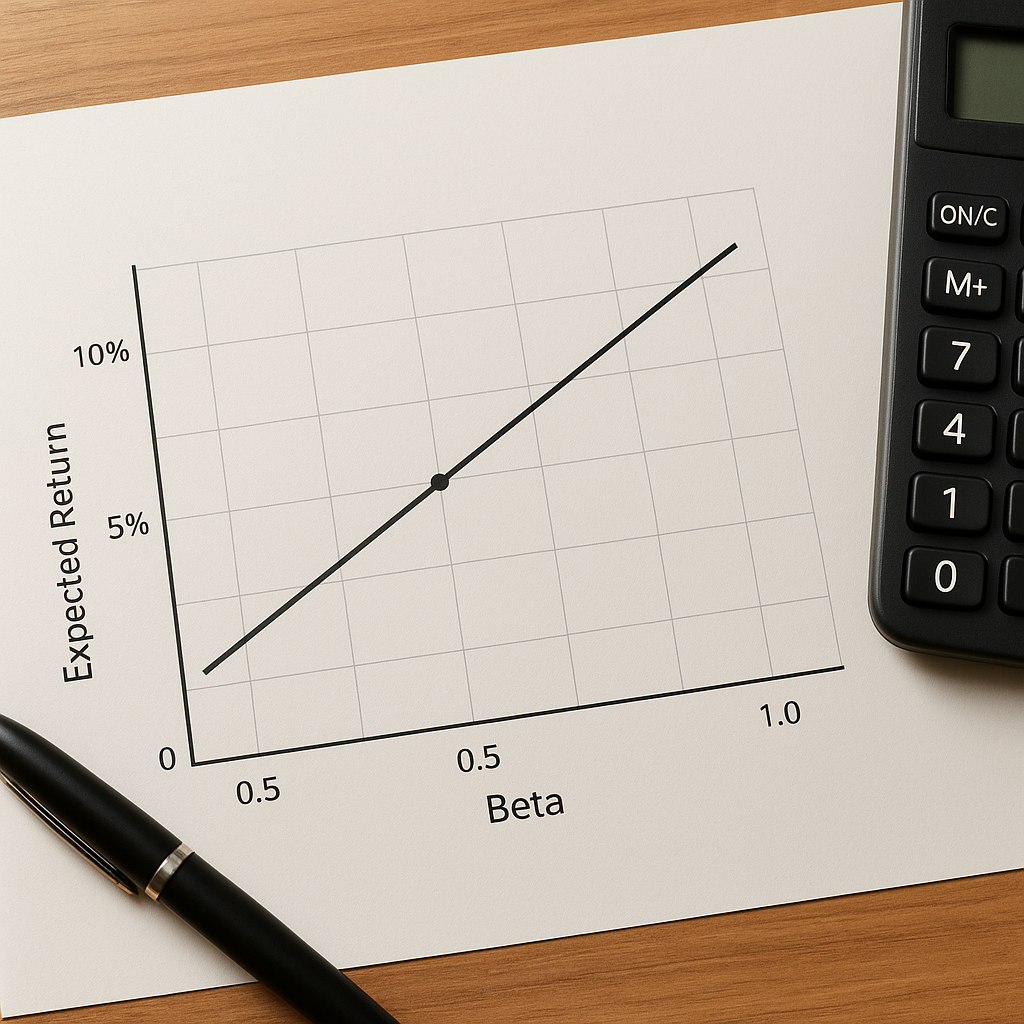
Beta mierzy wrażliwość stopy zwrotu danego aktywa na zmiany stopy zwrotu portfela rynkowego. Wysoka wartość beta (>1) oznacza, że aktywo zwykle reaguje z większą amplitudą niż rynek; beta <1 sugeruje niższą wrażliwość. Wartość beta równa 0 wskazuje brak związku z rynkiem, natomiast ujemna beta oznacza reakcję przeciwną do ruchów rynkowych.
Konstrukcja CAPM zakłada istnienie portfela rynku (market portfolio), który zawiera wszystkie aktywa w proporcji odpowiadającej ich wartości rynkowej. Na wykresie oczekiwanych stóp zwrotu względem ryzyka (wariancji lub odchylenia standardowego) pojawia się tzw. linia rynku kapitałowego (Capital Market Line, CML), a dla pojedynczych aktywów — Security Market Line (SML), która ukazuje zależność między beta a oczekiwaną stopą zwrotu. Różnica E(Rm) − Rf nazywana jest premią za ryzyko rynkowe.
Implikacje praktyczne i zastosowania
CAPM oferuje praktyczne narzędzia i intuicje wykorzystywane w finansach korporacyjnych, zarządzaniu portfelem oraz wycenie aktywów. Do najważniejszych zastosowań należą:
- określanie kosztu kapitału własnego firmy (stosowane w obliczaniu WACC),
- ocena efektywności menedżerów portfela przez analizę alfy i beta,
- budowa portfeli zgodnych z preferencjami ryzyka inwestora (alokacja aktywów),
- weryfikacja, czy dane aktywo jest przewartościowane czy niedowartościowane poprzez porównanie rzeczywistej stopy zwrotu z tą przewidywaną przez model.
W praktyce analitycy często wykorzystują CAPM do wyznaczania stopy dyskontowej dla projektów inwestycyjnych oraz do szacowania oczekiwanej stopy zwrotu z akcji w procesie wyceny. Jest również punktem wyjścia dla bardziej złożonych modeli wieloczynnikowych.
Badania empiryczne i krytyka
Pierwotne testy CAPM przyniosły mieszane rezultaty. Z jednej strony zaobserwowano, że beta rzeczywiście ma istotny związek z oczekiwaną stopą zwrotu, ale z drugiej — pojawiły się anomalie, które modelowi trudno wyjaśnić. Do najważniejszych problemów empirycznych należą:
- anomalie wielkości (efekt small-cap) — małe spółki dają często wyższe stopy zwrotu niż przewidywane przez CAPM,
- efekt wartości — spółki o niskich wskaźnikach cen do księgowej (low P/B) wykazują nadzwyczajne stopy zwrotu,
- anomalie dotyczące niskich i wysokich beta — badania wskazują, że spółki o niskiej beta często osiągają wyższe stopy zwrotu niż przewiduje model, co nazwano „low-beta anomaly”,
- krytyka Roll’a — Richard Roll wskazał, że testy CAPM są endogeniczne, ponieważ portfel rynku jest w praktyce nieobserwowalny (zawiera wszystkie aktywa), co komplikuje empiryczne weryfikacje modelu.
W efekcie wielu badaczy i praktyków przyznaje, że choć CAPM jest eleganckim i użytecznym narzędziem teoretycznym, to w zastosowaniach empirycznych wymaga uważnej interpretacji i korekt. Na jego korzyść przemawia prostota i jasny przekaz dotyczący roli ryzyka systematycznego, które nie może być wyeliminowane przez dywersyfikację i dlatego powinno być wynagradzane premią.
Ograniczenia i kryteria stosowania w praktyce
Ograniczenia CAPM wynikają zarówno z jego założeń, jak i z trudności estymacyjnych. Do głównych ograniczeń należą m.in.:
- trudność w precyzyjnym oszacowaniu bety i wymuszone założenie stacjonarności tego parametru w czasie,
- nieobserwowalność prawdziwego portfela rynku — często stosuje się indeksy giełdowe jako proxy, co może wprowadzać błąd,
- jednoczynnikowa natura modelu — CAPM uwzględnia tylko ryzyko rynkowe, ignorując inne czynniki wpływające na wycenę aktywów,
- założenie braku kosztów transakcyjnych i podatków, a także jednorodnych oczekiwań inwestorów, co w realnych warunkach rzadko ma miejsce.
Pomimo tych ograniczeń, w praktyce firmy i analitycy często używają CAPM jako punktu odniesienia. Jego prostota ułatwia komunikację wyników (np. wyznaczanie kosztu kapitału dla inwestorów instytucjonalnych), a jego intuicyjna interpretacja sprawia, że pozostaje cennym narzędziem w zestawie metod ilościowych.
Rozszerzenia, alternatywy i kierunki rozwoju
W odpowiedzi na empiryczne ograniczenia CAPM rozwinięto szereg alternatywnych i rozszerzonych modeli. Do najważniejszych należą:
- model APT (Arbitrage Pricing Theory) — podejście wieloczynnikowe, które nie wymaga istnienia portfela rynku i pozwala na identyfikację kilku czynników makroekonomicznych wpływających na stopy zwrotu,
- modele Fama-French — rozszerzenia uwzględniające dodatkowe czynniki, takie jak efekt wielkości (size) i efekt wartości (value), które znacząco poprawiły zdolność wyjaśniania różnic w stopach zwrotu,
- konsumpcyjny CAPM (CCAPM) oraz dynamiczne warianty, które próbują brać pod uwagę preferencje czasowe inwestorów i zmienne ryzyko agregatowe,
- podejścia behawioralne, które krytykują racjonalność uczestników rynku i sugerują, że anomalie wynikają z systematycznych odchyleń od racjonalnego zachowania.
W praktyce wybór modelu zależy od celu analizy, dostępnych danych i wymaganej precyzji. Wycena korporacyjna i analiza finansowa często zaczynają od CAPM i w razie potrzeby przechodzą do modeli wieloczynnikowych, aby lepiej uchwycić źródła ryzyka specyficzne dla danej próby aktywów.
Przykład obliczeniowy
Aby zilustrować działanie modelu, rozważmy prosty przykład. Załóżmy, że:
- Rf = 2% rocznie,
- E(Rm) = 8% rocznie,
- βi = 1,3.
Zgodnie z CAPM oczekiwana stopa zwrotu z aktywa i będzie wynosić:
E(Ri) = 2% + 1,3 * (8% − 2%) = 2% + 1,3 * 6% = 2% + 7,8% = 9,8%.
W tym przykładzie inwestor oczekiwałby około 9,8% rocznej stopy zwrotu, aby zrekompensować większą wrażliwość aktywa na ruchy rynku.
Wnioski dotyczące użyteczności modelu
Model CAPM pozostaje fundamentem teorii wyceny aktywów i jest szeroko stosowany w praktyce. Jego największą zaletą jest czytelność i jasne rozdzielenie wpływu ryzyka systemowego na oczekiwaną stopę zwrotu. Z drugiej strony, badania empiryczne wymusiły rozwój alternatywnych modeli i zwróciły uwagę na ograniczenia wynikające z rygorystycznych założeń. W kontekście decyzji inwestycyjnych warto traktować CAPM jako punkt wyjścia i narzędzie pomocnicze, a nie jedyną i ostateczną metodę wyceny.
Podsumowując, CAPM dostarcza istotnych wniosków dotyczących wyceny aktywów: premiuje się jedynie ryzyko, którego nie da się zdywersyfikować, a zrozumienie i prawidłowa estymacja beta oraz premii za ryzyko są kluczowe dla poprawnego wykorzystania modelu. Dalsze postępy w finansach koncentrują się na integracji dodatkowych czynników ryzyka i uwzględnieniu realnych ograniczeń rynkowych w celu uzyskania bardziej precyzyjnych wycen i lepszej alokacji kapitału.