Teoria portfela Markowitza – finanse

Teoria zaproponowana przez Harry’ego Markowitza zrewolucjonizowała podejście do inwestowania, przekształcając intuicyjne decyzje w formalny proces analityczny. W tym artykule omówię zasady tej teorii, jej matematyczne podstawy, praktyczne konsekwencje dla zarządzania aktywami oraz ograniczenia i rozszerzenia, które powstały w następstwie jej publikacji. Skupię się na kluczowych pojęciach, takich jak portfel, ryzyko i zwrot, a także pokażę, jak wpływają one na decyzje inwestycyjne w kontekście dywersyfikacja i optymalizacja.

Geneza i podstawowe założenia

Harry Markowitz opublikował swoje przełomowe prace pod koniec lat 50. XX wieku. Zamiast analizować pojedyncze aktywa, Markowitz zaproponował patrzenie na zbiór aktywów jako na całość — portfel. Kluczowa intuicja polegała na tym, że inwestor powinien oceniać aktywa nie tylko przez pryzmat oczekiwanego zwrotu, lecz także korelacji między nimi, co wpływa na całkowite ryzyko portfela.

Podstawowe założenia teorii można przedstawić następująco:

• Inwestor dąży do maksymalizacji oczekiwanego zwrotu przy zadanym poziomie ryzyka albo minimalizacji ryzyka przy zadanym oczekiwanym zwrocie.
• Ryzyko mierzone jest przez wariancję lub odchylenie standardowe stopy zwrotu portfela.
• Decyzje inwestycyjne opierają się na statycznym, jednoperiodycznym horyzoncie czasowym (analiza jednoperiodyczna).
• Rynki są efektywne w sensie, że inwestorzy są racjonalni i znają rozkłady oczekiwanych stóp zwrotu oraz kowariancje między aktywami.

Matematyczne podstawy: wariancja, kowariancja i formuła portfela

Formalny model Markowitza operuje pojęciami statystycznymi. Załóżmy, że mamy n aktywów. Wektorem wag portfela oznaczymy w = (w1, w2, …, wn), gdzie wi to udział kapitału zainwestowanego w aktywo i. Oczekiwany zwrot portfela to suma ważona oczekiwanych zwrotów poszczególnych aktywów:

• E(R_p) = sum_i wi * E(R_i).

Ryzyko portfela mierzone jest przez wariancję stopy zwrotu:

• Var(R_p) = w^T Σ w,

gdzie Σ to macierz kowariancji stóp zwrotu poszczególnych aktywów. Element Σ_ij to kowariancja między aktywem i i j. Dzięki temu można uchwycić efekt dywersyfikacja — jeżeli aktywa są słabo skorelowane lub ujemnie skorelowane, łączne ryzyko portfela może być istotnie mniejsze niż suma ryzyk poszczególnych pozycji.

Problem optymalizacji formułowany jest zwykle dwojako:

• Minimalizacja wariancji przy zadanym oczekiwanym zwrocie: minimize w^T Σ w subject to E(R_p) = R_target, sum_i wi = 1.
• Maksymalizacja oczekiwanego zwrotu przy ograniczeniu wariancji lub ograniczonym budżecie ryzyka: maximize E(R_p) – λ Var(R_p), gdzie λ odzwierciedla awersję inwestora do ryzyka.

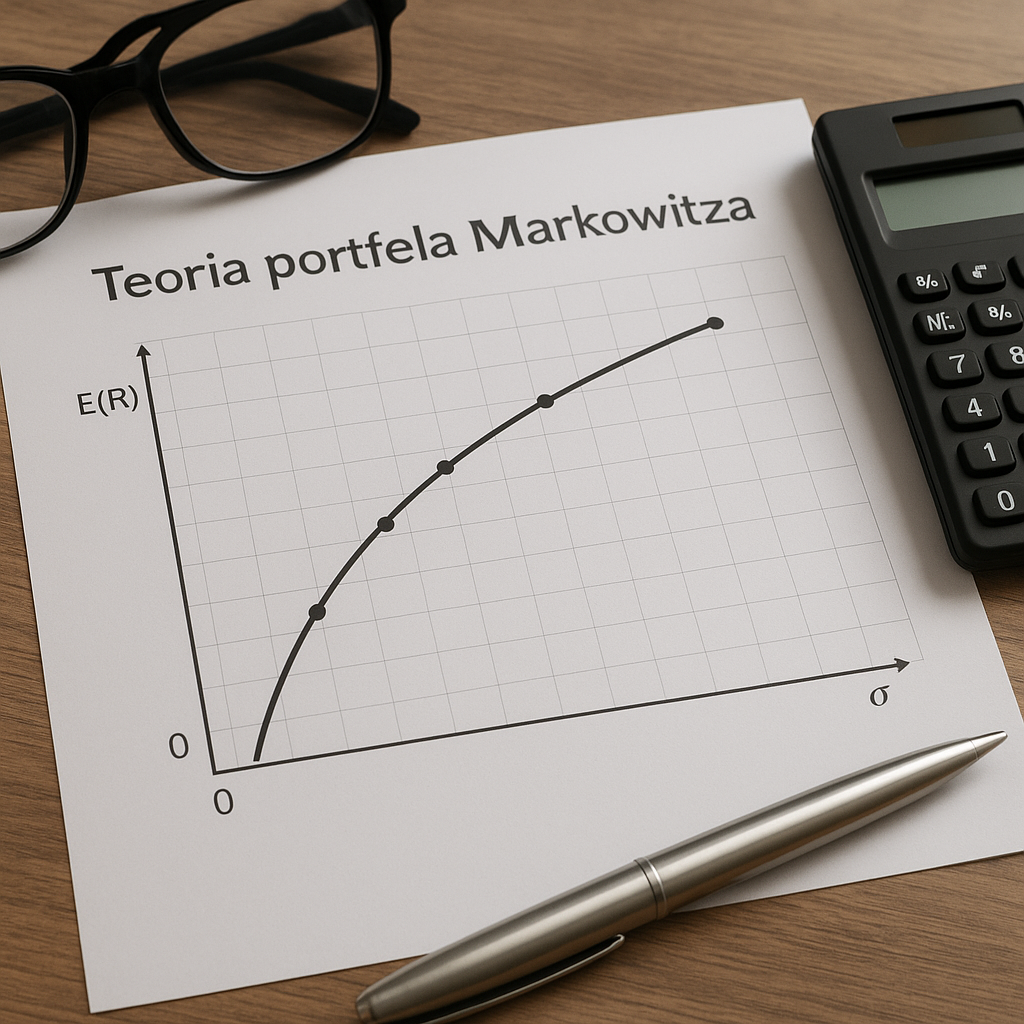
W ten sposób powstaje zbiór rozwiązań efektywnych, zwany efektywna granica (ang. efficient frontier): każda kombinacja na tej krzywej jest optymalna dla pewnego poziomu awersji do ryzyka — nie istnieje inny portfel, który miałby większy oczekiwany zwrot przy tym samym lub mniejszym ryzyku.

Interpretacja efektywnej granicy i rola korelacji

Efektywna granica to kluczowe narzędzie wyprowadzane z modelu Markowitza. Na wykresie przedstawiającym ryzyko (oś pozioma, zwykle odchylenie standardowe) i oczekiwany zwrot (oś pionowa), granica tej krzywej wyznacza najlepsze możliwe portfele. Portfel, który leży poniżej tej granicy, jest suboptymalny — istnieje inny portfel o takim samym ryzyku i wyższym zwrocie albo o takim samym zwrocie i niższym ryzyku.

Korelacje między aktywami determinują kształt granicy. Gdy wszystkie aktywa są doskonale skorelowane, efekt dywersyfikacja jest znikomy — granica sprowadza się do jednowymiarowej relacji. W przypadku niskich korelacji lub ujemnych kowariancji możliwe jest znaczące zmniejszenie wariancji portfela bez proporcjonalnej utraty oczekiwanego zwrotu. Dlatego analiza macierzy Σ i korelacji jest krytyczna przy konstruowaniu portfela.

Praktyczne zastosowania i implementacja

W praktyce implementacja modelu Markowitza wymaga estymacji szeregu parametrów: oczekiwanych stóp zwrotu dla każdego aktywa oraz macierzy kowariancji. Źródła danych to historyczne ceny, analizy fundamentalne, prognozy ekonomiczne i modele stochastyczne. Proces implementacyjny zazwyczaj przebiega według następujących kroków:

• Zebranie danych historycznych i wyczyszczenie serii (missing data, dzielenie akcji, dywidendy).
• Obliczenie historycznych stóp zwrotu oraz estymacja oczekiwanych zwrotów (średnie historyczne, modele prognostyczne).
• Estymacja macierzy kowariancja i korelacji; wybór horyzontu i częstotliwości (dziennych, tygodniowych, miesięcznych).
• Rozwiązanie problemu optymalizacja (np. przy użyciu metod kwadratowego programowania) z uwzględnieniem ograniczeń: brak krótkiej sprzedaży, limity wag, progi płynności itp.
• Testowanie wyników: backtesting, warunki rynkowe skrajne, stres testy oraz analiza stabilności wag portfela.

W praktyce pojawiają się trudności estymacyjne: historyczne średnie często są niestabilne, a macierz kowariancji może być źle uwarunkowana przy dużej liczbie aktywów i krótkich seriach danych. Z tego powodu wdrożenia profesjonalne często stosują techniki regularizacji, redukcji wymiarowości (np. analiza głównych składowych), albo wykorzystują bayesowskie uogólnienia estymacji parametrów, aby uzyskać bardziej stabilne wagi portfela.

Ograniczenia teorii Markowitza

Mimo teoretycznej elegancji, model nie jest pozbawiony krytyki:

• Estymacja parametrów — zwłaszcza oczekiwanych zwrotów — jest obarczona dużą niepewnością. Niewielkie błędy w szacunkach mogą prowadzić do znacznych zmian w proponowanych wagach.
• Normalność rozkładów — model wykorzystuje miary wariancji, które w sposób najprostszy mają sens przy symetrycznych rozkładach. Rynkowe stopy zwrotu wykazują skośność i grube ogony, co powoduje, że wariancja nie oddaje pełni ryzyka (np. ryzyko ogona, skrajne straty).
• Brak kosztów transakcyjnych i płynności — model w formie podstawowej nie uwzględnia kosztów kupna/sprzedaży ani ograniczeń płynności, które są kluczowe przy dynamicznej alokacji aktywów.
• Statyczny horyzont — klasyczny model jest jednoperiodyczny, co ogranicza użyteczność w długoterminowym zarządzaniu, gdzie oczekiwania zmieniają się w czasie.

Rozszerzenia i powiązane modele

W odpowiedzi na ograniczenia Markowitza rozwinięto szereg uogólnień i powiązanych teorii. Najważniejsze z nich to:

• Capital Asset Pricing Model (CAPM) — łączy koncepcję portfela rynkowego z mechaniką wyceny aktywów, wprowadzając pojęcie beta jako współczynnika ryzyka systemowego względem rynku.
• Black–Litterman — model, który poprawia estymację oczekiwanych zwrotów poprzez łączenie rynkowych oczekiwań (portfela rynkowego) z subiektywnymi prognozami inwestora, dając stabilniejsze i bardziej sensowne wagi portfela.
• Modele wielookresowe i dynamiczne — uwzględniają zmienność parametrów w czasie, koszty transakcyjne i ograniczenia portfelowe w horyzoncie wielookresowym.
• Metody oparte na ryzyku wartości zagrożonej (VaR), CVaR — zamiast wariancji uwzględniają ryzyko skrajnych strat, co lepiej odpowiada na asymetrię rozkładów zwrotów.

Praktyczny przykład konstruowania portfela

Aby zrozumieć proces, rozważmy uproszczony przykład z trzema aktywami A, B i C. Załóżmy, że estymowane oczekiwane roczne stopy zwrotu to 6%, 8% i 10%. Przyjmijmy uproszczoną macierz kowariancji (wartości pokazane jedynie w celach ilustracyjnych). Celem jest znalezienie portfela minimalizującego wariancję przy oczekiwanym zwrocie 8%.

W praktyce rozwiązanie tego typu zadania polega na użyciu optymalizatora kwadratowego. Występują tu standardowe ograniczenia: sum_i wi = 1 oraz, opcjonalnie, wi >= 0 (zakaz short selling). Wynik dostarczy wag wi, które zbalansują udział w bardziej dochodowych, ale bardziej zmiennych aktywach z udziałem aktywów o niższej zmienności, wykorzystując efekt dywersyfikacja opisany przez kowariancja.

Uwagi praktyczne: rebalancing, koszty i psychologia inwestora

Wdrażając teoretyczne wnioski w warunkach rynkowych, menedżerowie portfeli muszą uwzględnić:

• Politykę rebalancingu — częstotliwość dostosowywania wag wpływa na koszty transakcyjne i podatki. Zbyt agresywny rebalancing może zniwelować zyski wynikające z optymalizacji.
• Koszty i ograniczenia operacyjne — prowizje, bid-ask spread, ograniczenia inwestycyjne (np. limit udziału jednej spółki), a także minimalne transakcje/loty.
• Wybór horyzontu i częstotliwości danych — krótsze serie dają więcej obserwacji, ale mogą być bardziej szumne; dłuższe serie są stabilniejsze, lecz wolniej reagują na nowe informacje.
• Psychologia — awersja do strat i preferencje behawioralne wpływają na to, jak inwestorzy rzeczywiście realizują decyzje teoretyczne. Paradoks polega na tym, że model zakłada racjonalność, podczas gdy praktyka rynkowa często jest nią odległa.

Znaczenie teorii Markowitza dla zarządzania aktywami

Pomimo ograniczeń, teoria Markowitza pozostaje fundamentem współczesnego zarządzania portfelem. Daje ramy, które umożliwiają porównywanie strategii pod kątem relacji ryzyko–zwrot, a także stanowi punkt wyjścia do rozwinięć stosowanych w praktyce, takich jak modele uwzględniające koszty transakcyjne, ograniczenia płynności czy ryzyko ogona. Profesjonalni zarządzający korzystają z tej teorii, łącząc ją z narzędziami statystycznymi i modelami prognostycznymi, aby osiągnąć stabilne wyniki inwestycyjne.

Nowoczesne narzędzia i technologie wspierające optymalizację

Rozwój technologii obliczeniowych i dostęp do dużych zbiorów danych sprawiły, że implementacja idei Markowitza jest dziś praktycznie standardem w branży. Narzędzia te obejmują:

• Oprogramowanie do optymalizacji (np. biblioteki numeryczne, solvery QP),
• Techniki machine learning do estymacji oczekiwanych zwrotów i korelacji,
• Modele symulacyjne do oceny zachowania portfela w scenariuszach stresowych,
• Algorytmy redukcji wymiarów (PCA) w celu stabilizacji estymacji macierzy kowariancja.

Zastosowanie tych narzędzi bywa krytyczne, zwłaszcza gdy liczba dostępnych aktywów rośnie dramatycznie względem długości historii danych.

Aspekty regulacyjne i etyczne

W kontekście zarządzania aktywami teoria Markowitza nie wpływa jedynie na decyzje techniczne. Coraz istotniejsze stają się wymogi regulacyjne dotyczące ujawniania polityk inwestycyjnych, zarządzania ryzykiem i testów odporności portfeli na kryzysy. Dodatkowo inwestorzy instytucjonalni coraz częściej uwzględniają kryteria ESG (środowiskowe, społeczne i ładu korporacyjnego), co w praktyce oznacza dodanie kolejnych wymiarów do funkcji celu i ograniczeń optymalizacyjnych — tradycyjne miary ryzyko–zwrot muszą być wzbogacone o cele niefinansowe.

Wnioski praktyczne dla inwestora

Teoria portfela Markowitza uczy, że:

• Dywersyfikacja jest skuteczną metodą zarządzania ryzykiem, ale jej efektywność zależy od korelacji i jakości estymacji parametrów.
• W praktyce warto łączyć modelowo podejście optymalizacyjne z rozsądnymi ograniczeniami operacyjnymi i polityką rebalancingu.
• Wprowadzanie dodatkowych kryteriów (np. ryzyko ogona, ograniczenia ESG) wymaga adaptacji klasycznego modelu, ale nie podważa jego podstawowej wartości jako ramy analitycznej.
• Stabilność wag portfela i wiarygodność wyników zależą od jakości danych i metod estymacji — techniki regularizacyjne i bayesowskie poprawiają praktyczne zastosowanie metody.