Model Blacka–Scholesa – finanse

Model Blacka–Scholesa jest jednym z najbardziej wpływowych narzędzi w teorii wyceny instrumentów pochodnych. Jego rozwój znacząco zmienił podejście do zarządzania ryzykiem i wyceny opcji, wprowadzając formalną metodologię łączącą probabilistykę, rachunek różniczkowy i ekonomię. W tekście tym omówię genezę modelu, podstawowe założenia, matematyczne podstawy, praktyczne zastosowania, ograniczenia oraz najważniejsze rozszerzenia i alternatywy stosowane we współczesnych finansach.

Geneza i znaczenie modelu

Początki modelu sięgają pracy autorstwa Fishera Blacka i Myrona Scholesa z 1973 roku, a także późniejszych uzupełnień przez Roberta Mertona. Jego powstanie było reakcją na potrzebę znalezienia spójnej metody wyceny opcji europejskich w sposób, który byłby nie tylko intuicyjny, ale również matematycznie ugruntowany. Model przyczynił się do powstania rozległego rynku instrumentów pochodnych i stał się standardem referencyjnym przy wycenie wielu klas aktywów.

Krótka historia

1973: publikacja artykułu Black & Scholes z formułą wyceny opcji
1973–1974: uzupełnienia i matematyczne uszczegółowienia przez Roberta Mertona
lata 80. i 90.: szerokie przyjęcie w bankach inwestycyjnych i funduszach hedgingowych
współcześnie: baza do dalszych rozszerzeń, takich jak modele zmienności stochastycznej czy modele skoków

Podstawowe założenia i intuicja ekonomiczna

Aby zrozumieć, jak działa model Blacka–Scholesa, warto poznać jego kluczowe założenia. Są to uproszczenia, które umożliwiają otrzymanie zamkniętej postaci rozwiązania, lecz równocześnie narzucają ograniczenia co do zakresu zastosowań.

Brak arbitrażu — rynek nie dopuszcza możliwości bezryzykownego zysku poprzez arbitraż portfeli.
Ciągłość cen — ceny instrumentów podlegają ciągłemu procesowi stochastycznemu bez skoków.
Stopy procentowe są stałe i znane (przynajmniej w okresie wygaśnięcia opcji).
Brak kosztów transakcyjnych i podatków; możliwy jest nieograniczony handel krótkiej sprzedaży.
Zmienność instrumentu bazowego jest stała (σ) w czasie.

Intuicyjnie model wykorzystuje koncepcję replikacji — konstruowania portfela złożonego z akcji i lokat pieniężnych, którego wartość w każdym momencie jest równa wartości opcji. Dzięki temu, skoro portfel replikuje payoff opcji, jego cena nie może odbiegać od teoretycznej wartości opcji bez naruszenia warunku braku arbitrażu.

Matematyczne podstawy i wzór Blacka–Scholesa

W sercu modelu znajduje się założenie, że cena instrumentu bazowego S(t) podąża za geometrycznym ruchem Browna z dryftem μ i zmiennością σ, co zapisuje się równaniem różniczkowym stochastycznym:

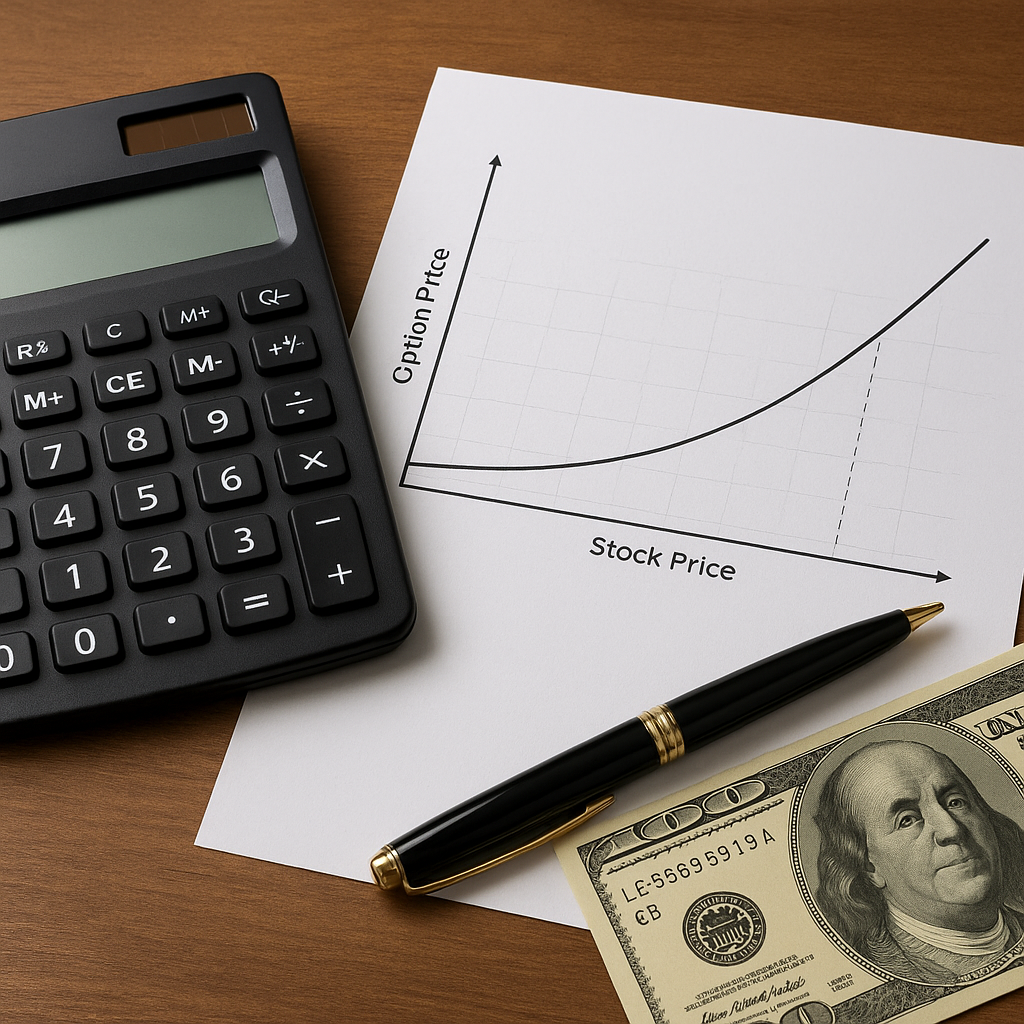
Szczegóły równania i wyprowadzenia prowadzą do utworzenia równania różniczkowego cząstkowego (PDE), które musi spełniać funkcja ceny opcji. Rozwiązaniem tej PDE dla opcji europejskiej typu call jest dobrze znana formuła:

c = S0 Φ(d1) − K e^{-rT} Φ(d2)
d1 = (ln(S0/K) + (r + 0.5 σ^2) T) / (σ sqrt(T))
d2 = d1 − σ sqrt(T)

Gdzie Φ oznacza dystrybuantę standardowego rozkładu normalnego, S0 to bieżąca cena aktywa bazowego, K — cena wykonania, r — wolna od ryzyka stopa procentowa, σ — zmienność, a T — czas do wygaśnięcia (wyrażony w latach).

Rola każdego parametru

S0: określa bezpośrednią ekspozycję — im wyższa cena bazowa, tym bardziej opcja call jest wartościowa.
K: cena wykonania; decyduje o relacji moneyness opcji.
r: wpływa na wartość zdyskontowanego payoffu.
σ: kluczowy parametr determinujący wartość opcji; większa zmienność zwiększa wartość opcji.
T: czas do wygaśnięcia; dłuższy czas zazwyczaj zwiększa wartość opcji ze względu na większą niepewność.

Greeks — miary wrażliwości ceny opcji

W praktyce wycena to tylko pierwszy krok. Kluczowe jest zrozumienie, jak cena opcji reaguje na zmiany parametrów rynkowych. Miary te nazywamy wspólnie Greeks i są niezbędne w zarządzaniu ryzykiem.

Delta — wrażliwość ceny opcji na niewielką zmianę ceny aktywa bazowego. Dla calla delta ∈ (0,1).
Gamma — miara zmiany delty względem ceny bazowej; informuje o nieliniowości ekspozycji.
Vega — wrażliwość ceny opcji na zmianę zmienności σ.
Theta — miara „erosji” wartości opcji w czasie (czasowy decay).
Rho — wrażliwość na zmianę stopy wolnej od ryzyka r.

Zrozumienie i obliczanie tych miar umożliwia jednoczesne zarządzanie wieloma wymiarami ryzyka — uczestnicy rynku mogą delta-hedgować swoje pozycje, monitorować ekspozycję na zmienność czy planować działania w sytuacji zmiany stóp procentowych.

Praktyczne zastosowania i implementacja

Model Blacka–Scholesa jest wykorzystywany szeroko — od prostych wycen pojedynczych opcji po systemy handlu algorytmicznego i zarządzanie portfelem opcyjnym. W praktycznej implementacji pojawiają się jednak pewne wyzwania i adaptacje.

Wycena i implied volatility

Jednym z najważniejszych zastosowań jest wyznaczanie tzw. implied volatility — odwrotne użycie modelu: znając cenę rynkową opcji, wyliczamy taką wartość σ, która sprawia, że formuła Blacka–Scholesa zwróci obserwowaną cenę. Implied volatility stała się kluczowym wskaźnikiem rynkowego postrzegania ryzyka i często jest wykorzystywana do:

porównywania wycen rynkowych i modeli;
tworzenia krzywych implikowanej zmienności względem terminu i moneyness;
strategii handlowych opartych na anomaliach w rozkładzie implikowanej zmienności.

Numerical methods i hedging

Choć formuła analityczna istnieje dla prostych opcji europejskich, praktyka wymaga często stosowania metod numerycznych: metoda różnic skończonych, symulacje Monte Carlo, oraz algorytmy optymalizacji do kalibracji modelu. Hedging oparty na delcie wymaga natomiast ciągłej rewizji pozycji, co w realnym świecie odbywa się w dyskretnych odstępach czasu i generuje koszty transakcyjne.

Ograniczenia modelu

Mimo swojej elegancji, model Blacka–Scholesa opiera się na uproszczeniach, które nie zawsze są spełnione na rynkach finansowych. Najważniejsze ograniczenia to:

Stała zmienność — empirycznie zmienność jest zależna od czasu i poziomu cen (efekt skrzywienia i uśmiechu zmienności).
Brak skoków — ceny aktywów mogą doświadczać nagłych, dużych ruchów, które nie są uwzględnione w procesie geometrycznego ruchu Browna.
Brak kosztów transakcyjnych oraz niemożność nieograniczonej krótkiej sprzedaży — upraszczające założenia rzadko spełnione w praktyce.
Stopy procentowe oraz dywidendy mogą być niestabilne i trudne do modelowania w prosty sposób.

Konsekwencją tych ograniczeń jest, że rynkowe ceny opcji często odbiegają od cen teoretycznych Blacka–Scholesa, co prowadzi do obserwacji takich zjawisk jak skew i smile zmienności. Te zjawiska stały się impulsem do rozwijania bardziej zaawansowanych modeli.

Rozszerzenia i alternatywne modele

Aby lepiej oddać rzeczywistość rynkową, badacze i praktycy rozwinęli kilka ważnych rozszerzeń modelu:

Modele zmienności stochastycznej (np. Heston) — w których zmienność sama podlega procesowi losowemu, co pozwala wyjaśnić strukturę implikowanej zmienności.
Modele skoków (np. Merton Jump-Diffusion) — dodają składową skokową do procesu ceny, co umożliwia uchwycenie ryzyk nagłych ruchów cenowych.
Modele lokalnej zmienności (Dupire) — zakładają, że zmienność jest funkcją ceny i czasu, dopasowując model do obserwowanego uśmiechu zmienności.
Metody numeryczne i hybrydowe — łączące symulacje Monte Carlo z technikami przyspieszającymi kalibrację i wycenę złożonych instrumentów.

Kalibracja modeli i praktyczne wyzwania

Kalibracja oznacza dopasowanie parametrów modelu do obserwowanych cen rynkowych. W przypadku Blacka–Scholesa najczęściej kalibruje się implied volatility dla poszczególnych terminów i strike’ów, tworząc powierzchnię zmienności. Dla bardziej złożonych modeli proces ten może obejmować optymalizację wielu parametrów naraz i wiąże się z wyzwaniami:

problem lokalnych minimów — funkcja kosztu może mieć wiele minimów, co utrudnia znalezienie globalnego rozwiązania;
złożoność obliczeniowa — symulacje i metody numeryczne są kosztowne czasowo;
zależność od jakości danych rynkowych — brak płynności lub błędy w notowaniach wpływają na stabilność kalibracji;
obsługa instrumentów egzotycznych — wymagają często doprecyzowania modelu lub przyjęcia dodatkowych założeń.

Przykładowe techniki kalibracyjne

metody najmniejszych kwadratów i ważonych najmniejszych kwadratów;
algorytmy genetyczne i heurystyczne do wyszukiwania rozwiązań globalnych;
metody gradientowe oraz ich warianty (Levenberg–Marquardt);
przyspieszone symulacje Monte Carlo, np. z użyciem wariancji redukujących technik.

Empiria i testy rynkowe

Empiryczne badania wykazują, że model Blacka–Scholesa dostarcza użytecznych przybliżeń, ale nie tłumaczy wszystkich obserwowanych zjawisk rynkowych. Szczególnie widoczne są:

Uśmiech zmienności — implikowana zmienność zależy od strike i czasu do wygaśnięcia;
zmienność historyczna nie zawsze koreluje z implikowaną;
niektóre rynki (np. towary, waluty z interwencjami) wykazują cechy trudne do odzwierciedlenia w prostych modelach.

Badania porównawcze sugerują, że modele rozszerzone (stochastyczna zmienność, skoki) lepiej dopasowują się do danych rynkowych, zwłaszcza gdy celem jest wycena instrumentów egzotycznych lub pełne odwzorowanie powierzchni implikowanej zmienności.

Zastosowania w zarządzaniu ryzykiem i regulacjach

Wyceny opcji za pomocą Blacka–Scholesa są wykorzystywane nie tylko w handlu, lecz także w raportowaniu ryzyka i wymogach kapitałowych instytucji finansowych. Modele te wpływają na:

strategię hedgingową i zarządzanie portfelem;
ocenę wartości godziwej instrumentów pochodnych;
wyznaczanie kapitału ekonomicznego w modelach wewnętrznych;
systemy wyceny i raportowania w bankach i funduszach inwestycyjnych.

W praktyce instytucje często używają wielu modeli jednocześnie, porównując wyniki i stosując konserwatywne założenia przy ocenie ryzyka rynkowego.

Wnioski dotyczące użytkowania modelu

Model Blacka–Scholesa pozostaje fundamentem współczesnej teorii wyceny opcji i narzędziem dydaktycznym, bez którego trudno wyobrazić sobie nauczanie finansów matematycznych. Jego siła tkwi w eleganckim połączeniu teorii i praktyki, umożliwiając zrozumienie podstawowych mechanizmów wyceny i hedgingu. Zarazem, jego ograniczenia sprawiają, że użytkownicy powinni stosować go świadomie, często łącząc z bardziej zaawansowanymi modelami i podejściami empirycznymi.

Kluczowe pojęcia do dalszego studiowania

implied volatility
delta-hedging
modele stochastycznej zmienności
skok-dyfuzyjne
kalibracja